墙裂推荐(怎么判断连通图)连通图判定,判断图的连通性的三种方法:DFS、BFS 和并查集,判断图是否连通java,
1 什么是结点的连通性?
若图 G 中两个不同的结点 u 和 v 存在路径 e,则称结点 u 和结点 v 连通。
2 什么是图的连通性?
若图 G 中任意两个结点连通,则称图 G 连通。
3 怎样判断图的连通性?
判断图的连通性的常见方法有三种:DFS、BFS 和并查集。
3.1 DFS
深度优先遍历得到的是图的一个连通分量。
算法流程:
从某个结点 v 出发,访问结点 v,并令 vis[v] = 1;查找 v 的所有邻接点 i,若结点 i 并未被访问过(vis[i] = 0),则从结点 i 出发,深度优先遍历图,转至步骤(1)。递归结束后,遍历 vis 数组,若数组中有一个值不为 1,则说明该点未被访问,图不连通。3.2 BFS
算法流程:
从某个结点 v 出发,将结点 v 放入队列 q 中;队列不空时,弹出队首结点 v;如果结点 v 没被访问过,查找 v 的所有邻接点 i;如果结点 i 没被访问过,放入队列 q 中;如果结点 i 已被访问,跳过。如果结点 v 已被访问,跳过。标记结点 v 已被访问(容易遗漏!!!)。队列为空时,遍历 vis 数组,若数组中有一个值不为 1,则说明该点未被访问,图不连通。3.3 并查集
并查集可以简单理解为找根结点,使用 father 数组记录每个结点的根节点。
算法流程:
初始化每个结点的根节点为结点本身;(可使用 iota() 函数)从某个结点 v 开始,查找 v 的所有邻接点 i,如果结点 v 和结点 i 的根节点不同(father[v] != father[i]),则把两个结点的根节点设为下标较小的根节点(father[v] = father[i] = min(father[v], father[i]))。循环结束时,遍历 father 数组,若数组中有一个值不为 0,则说明该点的根节点并不是 0 号结点,图不连通。3.4 比较
DFS 和 BFS 都是记录结点是否已访问,而并查集是记录每个结点的根节点。三种算法都需要查询当前结点的所有邻接点,因而建议以邻接表的形式存储图。三种算法的时间复杂度和空间复杂度如下表所示,其中 E 为边的数目,V 为结点的数目。
4 代码
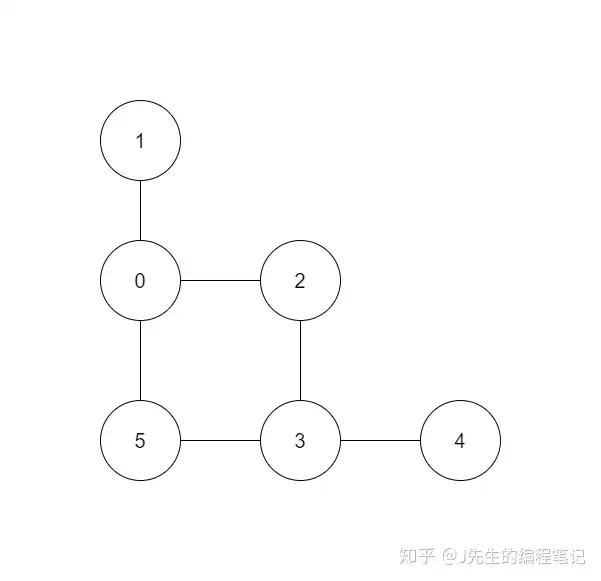
#include <iostream>#include <numeric>#include <queue>#include <vector>using namespace std;vector<vector<int>> g;int n;vector<int> vis;vector<int> father;void dfs(int v) {cout << v << " ";vis[v] = 1;for (int i = 0; i < g[v].size(); i++) {if (!vis[g[v][i]]) {dfs(g[v][i]);}}}void bfs() {queue<int> q;q.push(0);while (!q.empty()) {int v = q.front();cout << v << " ";q.pop();if (!vis[v]) {for (int i = 0; i < g[v].size(); i++) {if (!vis[g[v][i]]) {q.push(g[v][i]);}}}vis[v] = 1;}}int Find(int x) {int a = x;while (x != father[x]) {x = father[x];}while (a != father[a]) {int z = a;a = father[a];father[a] = x;}return x;}void Union(int a, int b) {int fA = Find(a);int fB = Find(b);father[a] = father[b] = min(fA, fB);}int main() {n = 6;g = vector<vector<int>>(n, vector<int>());// 插入 6 条边(双向) g[0].push_back(1);g[0].push_back(2);g[0].push_back(5);g[1].push_back(0);g[2].push_back(0);g[2].push_back(3);g[3].push_back(2);g[3].push_back(4);g[3].push_back(5);g[4].push_back(3);g[5].push_back(0);g[5].push_back(3);// DFS vis = vector<int>(n, 0);dfs(0);cout << endl;//0 1 2 3 4 5// BFS vis = vector<int>(n, 0);bfs();cout << endl;//0 1 2 5 3 3 4// Union-Find Set father = vector<int>(n);iota(father.begin(), father.end(), 0);for (int i = 0; i < n; i++) {for (int j = 0; j < g[i].size(); j++) {if (father[i] != father[g[i][j]]) {cout << i << " " << g[i][j] << endl;Union(i, g[i][j]);}}}//0 1 //0 2 //0 5 //2 3 //3 4// 可通过求和判断数组内所有元素是否都为 0: cout << (accumulate(father.begin(), father.end(), 0) == 0) << endl; //1 return 0;}
References
无向图连通性判断的五种方法(BFS、DFS、Union-find、Warshell、Tarjan)版权申明
本文系作者 @河马 原创发布在河马博客站点。未经许可,禁止转载。



暂无评论数据